Topological sort

这是coursera上的princeton算法课程的读书笔记å 这个princeton公开课的源地址，如果对课程感兴趣可以在coursera上搜这一门课程。

DAG => Directed acyclic graph. 有向无环图

Topological sort. Redraw DAG so all edges point upwards.

可以从下面的两张图看toplogy sort的实际效果:

排序之前:

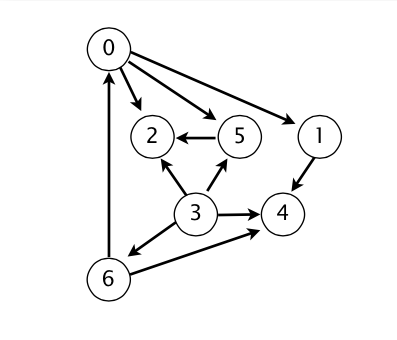
排序之后:

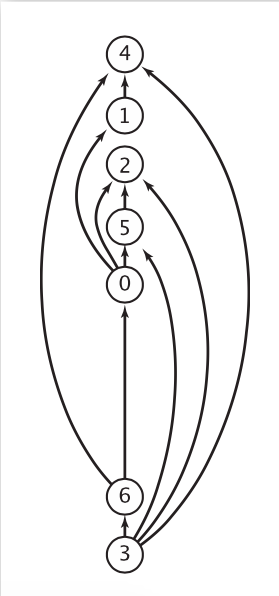
排序之后，所有的节点都”向上”

澄清

toplogy sort和常见的排序算法本质上是有区别的。排序算法通常是对数组或者链表这样的线性数据结构，默认是从下标0开始访问的，而图是没有这样的限制。toplogy sort只是”强制”给图规定了一个顺序，让图能够用数组的方式去理解。

##Topological sort的证明 反转的DFS postorder是DAG的topological顺序

证明如下：考虑任意的边 v->w。当dfs(v)被调用 有下面几种情况

Case 1 => dfs(w)已经被调用，并且已经被返回。因此w在v之前被返回。

Case 2 => dfs(w)没有被调用。那么，由于v->w有直接的边或者非直接的边，那么，一定会调用dfs(w)。然后w也被返回。

Case 3 => dfs(w)已被调用，但是没有被返回，这样就会存在一个w ->v的边，构成环了，然后就会与DAG矛盾。

Directed cycle detection

如何检测一个环

如果监测一个图有没有环? Proposition：A digraph has a topological order iff no directed cycle 命题: 一个图，如果有拓扑顺序，那么就没有环 证明: 如果有环，那么就没有拓扑顺序（在上面的拓扑顺序已经证明了这一点） 如果没有环，那么就可以找到一个拓扑顺序，使用DFS-based算法可以找到这样的拓扑顺序。

还有其他方法吗？ 当然有。在学习链表的时候，有可能面临过这样的问题: 怎么判断链表是否有环？ 一种方法是，遍历一个链表，一个采用步数为2，一个采用步数为1，如果他们在某个时候相遇(刚好走到同一个节点)，那么，这个链表是有环的。

#TODO 图有环的其他方法